}$ means that sum over nearby spin pairs, and $\\sigma$ is the $z$-direction spin operator."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"But since $\\sigma_i$ commute with each other, the Hamiltonian just acts as number. We will treat this model as a \"classical\" system and treat $\\sigma_i$ as a variable taking it's value of $\\pm 1$."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
},
"tags": []
},
"source": [
"The existing of $J$ term can explain the difference between ferromagnetism behavior and paramagnetism behavior."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
},
"tags": []
},
"source": [
"### 3.1 Ising model on 2D finite square lattice"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
},
"tags": []
},
"source": [
"We introduce the periodic boundary condition on a $N \\times N$ lattice, so that each spin always interacts with 4 spins."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
},
"tags": []
},
"source": [
"Thus the model is defined on a torus.\n",
"\n",
""
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
},
"tags": []
},
"source": [
"We'll also assuming that\n",
"$ B = 0, \\quad J=1$."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
},
"tags": []
},
"source": [
"#### 3.1.1 the Analytical Solution"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Just post to show it...\n",
"\n",
"I get the partition function using mathematica for $N=8$ lattice:"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
},
"tags": []
},
"source": [
"$$ Z(\\beta) = \\mathrm{e}^{2N^2 \\beta} \\tilde{Z}(\\mathrm{e}^{-2 \\beta}),$$\n",
"where $\\tilde{Z}(x)$ is a polynomial:"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
},
"tags": []
},
"source": [
"$$ \\tilde{Z}(x) = 2 x^{128}+128 x^{124}+256 x^{122}+4672 x^{120}+17920 x^{118}+145408 x^{116}+712960 x^{114}+4274576 x^{112}+22128384 x^{110}+118551552 x^{108}+610683392 x^{106}+3150447680 x^{104}+16043381504 x^{102}+80748258688 x^{100}+396915938304 x^{98}+1887270677624 x^{96}+8582140066816 x^{94}+36967268348032 x^{92}+149536933509376 x^{90}+564033837424064 x^{88}+1971511029384704 x^{86}+6350698012553216 x^{84}+18752030727310592 x^{82}+50483110303426544 x^{80}+123229776338119424 x^{78}+271209458049836032 x^{76}+535138987032308224 x^{74}+941564975390477248 x^{72}+1469940812209435392 x^{70}+2027486077172296064 x^{68}+2462494093546483712 x^{66}+2627978003957146636 x^{64}+2462494093546483712 x^{62}+2027486077172296064 x^{60}+1469940812209435392 x^{58}+941564975390477248 x^{56}+535138987032308224 x^{54}+271209458049836032 x^{52}+123229776338119424 x^{50}+50483110303426544 x^{48}+18752030727310592 x^{46}+6350698012553216 x^{44}+1971511029384704 x^{42}+564033837424064 x^{40}+149536933509376 x^{38}+36967268348032 x^{36}+8582140066816 x^{34}+1887270677624 x^{32}+396915938304 x^{30}+80748258688 x^{28}+16043381504 x^{26}+3150447680 x^{24}+610683392 x^{22}+118551552 x^{20}+22128384 x^{18}+4274576 x^{16}+712960 x^{14}+145408 x^{12}+17920 x^{10}+4672 x^8+256 x^6+128 x^4+2 $$"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
},
"tags": []
},
"source": [
"OK, I think you already don't want to see any more equation like this, let's move to the MC method..."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
},
"tags": []
},
"source": [
"#### 3.1.2 Python Time"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
},
"tags": []
},
"source": [
"- Use a table `s[i,j]` to save spins;\n",
"- Set any initial state;\n",
"- Randomly choose `i,j` to flip the spin;\n",
"- $\\Delta E = -J(\\text{nearby sum}) \\times \\Delta s_{ij} = 2J(\\text{nearby sum})*s_{ij}$;\n",
"- When `random()` ${}< \\mathrm{e}^{-\\Delta E/T}$, accept the flip;\n",
"- Let the computer repeat!"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
},
"tags": []
},
"source": [
"##### Test"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {
"ExecuteTime": {
"end_time": "2022-04-19T14:30:13.513885Z",
"start_time": "2022-04-19T14:30:13.507179Z"
}
},
"outputs": [],
"source": [
"def gqlist(N):\n",
"\tif N==2:\n",
"\t\treturn [2, 0, 12, 0, 2]\n",
"\telif N== 4:\n",
"\t\treturn [2,0,32,64,424,1728,6688,13568,20524,13568,6688,1728,424,64,32,0,2]\n",
"\telif N== 8:\n",
"\t\treturn [2, 0, 128, 256, 4672, 17920, 145408, 712960, 4274576, 22128384, 118551552, 610683392, 3150447680, 16043381504, 80748258688, 396915938304, 1887270677624, 8582140066816, 36967268348032, 149536933509376, 564033837424064, 1971511029384704, 6350698012553216, 18752030727310592, 50483110303426544, 123229776338119424, 271209458049836032, 535138987032308224, 941564975390477248, 1469940812209435392, 2027486077172296064, 2462494093546483712, 2627978003957146636, 2462494093546483712, 2027486077172296064, 1469940812209435392, 941564975390477248, 535138987032308224, 271209458049836032, 123229776338119424, 50483110303426544, 18752030727310592, 6350698012553216, 1971511029384704, 564033837424064, 149536933509376, 36967268348032, 8582140066816, 1887270677624, 396915938304, 80748258688, 16043381504, 3150447680, 610683392, 118551552, 22128384, 4274576, 712960, 145408, 17920, 4672, 256, 128, 0, 2]\n",
"def E_theory(T,N=16):\n",
"\tx = np.exp(-2/T)\n",
"\tZtitle = 0\n",
"\tglist = gqlist(N)\n",
"\tfor i in range(N*N+1):\n",
"\t\tZtitle += glist[i]*np.power(x,2*i)\n",
"\tthE = 0\n",
"\tfor i in range(N*N+1):\n",
"\t\tthE += i*(glist[i]*np.power(x,2*i)/(Ztitle*N*N))\n",
"\tthE *= 4\n",
"\tthE -= 2\n",
"\treturn thE"
]
},
{
"cell_type": "code",
"execution_count": 42,
"metadata": {
"slideshow": {
"slide_type": "subslide"
},
"tags": []
},
"outputs": [],
"source": [
"from rich.progress import track\n",
"from rich.console import Console\n",
"from rich.table import Table\n",
"def Ising2D_E(T,moves,N=16):\n",
"\tJ = 1\n",
"\tB = 0\n",
"\n",
"\tslist = np.ones((N,N), dtype=int)\n",
"\tenergylist = np.empty(moves)\n",
"\tenergy = - 2*J * N * N\n",
"\tacp = 0\n",
"\n",
"\tfor step in track(range(moves)):\n",
"\t\t[i,j] = rng.integers(N,size=2)\n",
"\t\tdE = 2*J*(slist[(i-1)%N,j] + slist[(i+1)%N,j] + slist[i,(j-1)%N] + slist[i,(j+1)%N])*slist[i,j]\n",
"\t\tif rng.random() < np.exp(-dE/T):\n",
"\t\t\tacp += 1\n",
"\t\t\tslist[i,j] *= -1\n",
"\t\t\tenergy += dE\n",
"\t\tenergylist[step] = energy\n",
"\teth = E_theory(N=N,T=T)\n",
"\temc = np.mean(energylist[moves//2:])/(N*N)\n",
"\n",
"\ttable = Table(title=\"energy of 2D Ising\")\n",
"\ttable.add_column(\"T\", style = \"green\")\n",
"\ttable.add_column(\"theoretical\", style=\"cyan\")\n",
"\ttable.add_column(\"Monte Calor\", style=\"magenta\")\n",
"\ttable.add_column(\"persentage error\", style = \"blue\")\n",
"\ttable.add_row(str(T),str(eth), str(emc), str(100*(emc-eth)/eth)+\"%\")\n",
"\n",
"\tconsole = Console()\n",
"\tconsole.print(table)\n",
"\treturn energylist/(N*N)"
]
},
{
"cell_type": "code",
"execution_count": 46,
"metadata": {
"slideshow": {
"slide_type": "fragment"
},
"tags": []
},
"outputs": [
{
"data": {
"text/html": [
"Working... ━━━━━━━━━━━━━━━━━━━━━━━━━━╸━━━━━━━━━━━━━ 67% 0:00:01\n",
"\n"
],
"text/plain": [
"Working... \u001b[38;2;249;38;114m━━━━━━━━━━━━━━━━━━━━━━━━━━\u001b[0m\u001b[38;2;249;38;114m╸\u001b[0m\u001b[38;5;237m━━━━━━━━━━━━━\u001b[0m \u001b[35m 67%\u001b[0m \u001b[36m0:00:01\u001b[0m\n"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/html": [
"\n"
],
"text/plain": []
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/html": [
"\n",
"\n"
],
"text/plain": [
"\n"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/html": [
" energy of 2D Ising \n",
"┏━━━┳━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━┓\n",
"┃ T ┃ theoretical ┃ Monte Calor ┃ persentage error ┃\n",
"┡━━━╇━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━┩\n",
"│ 5 │ -0.4283680589440815 │ -0.41901625 │ -2.1831247098893214% │\n",
"└───┴─────────────────────┴─────────────┴──────────────────────┘\n",
"\n"
],
"text/plain": [
"\u001b[3m energy of 2D Ising \u001b[0m\n",
"┏━━━┳━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━┓\n",
"┃\u001b[1m \u001b[0m\u001b[1mT\u001b[0m\u001b[1m \u001b[0m┃\u001b[1m \u001b[0m\u001b[1mtheoretical \u001b[0m\u001b[1m \u001b[0m┃\u001b[1m \u001b[0m\u001b[1mMonte Calor\u001b[0m\u001b[1m \u001b[0m┃\u001b[1m \u001b[0m\u001b[1mpersentage error \u001b[0m\u001b[1m \u001b[0m┃\n",
"┡━━━╇━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━┩\n",
"│\u001b[32m \u001b[0m\u001b[32m5\u001b[0m\u001b[32m \u001b[0m│\u001b[36m \u001b[0m\u001b[36m-0.4283680589440815\u001b[0m\u001b[36m \u001b[0m│\u001b[35m \u001b[0m\u001b[35m-0.41901625\u001b[0m\u001b[35m \u001b[0m│\u001b[34m \u001b[0m\u001b[34m-2.1831247098893214%\u001b[0m\u001b[34m \u001b[0m│\n",
"└───┴─────────────────────┴─────────────┴──────────────────────┘\n"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"image/svg+xml": [
"\n",
"\n",
"\n"
],
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"elist = Ising2D_E(5, 100000, N=8)\n",
"plt.plot(elist)\n",
"%config InlineBackend.figure_format='svg'\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
},
"tags": []
},
"source": [
"##### (1) Energy"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"ExecuteTime": {
"end_time": "2022-04-19T14:29:47.508655Z",
"start_time": "2022-04-19T14:29:47.292419Z"
}
},
"outputs": [],
"source": [
"from scipy.stats import chi2,halfnorm,t\n",
"\n",
"def Ising2D_E_vec(T,moves,N=16):\n",
"\tJ = 1\n",
"\tB = 0\n",
"\tNT=T.size\n",
"\n",
"\tslist = np.ones((N,N,NT), dtype=int)\n",
"\tenergylist = np.empty((moves,NT))\n",
"\tenergy = - 2*J * N * N\n",
"\n",
"\tfor step in track(range(moves)):\n",
"\t\t[i,j] = rng.integers(N,size=2)\n",
"\t\tdE = 2*J*(slist[(i-1)%N,j] + slist[(i+1)%N,j] + slist[i,(j-1)%N] + slist[i,(j+1)%N])*slist[i,j]\n",
"\t\tboollist = rng.random() < np.exp(-dE/T)\n",
"\t\tslist[i,j] *= 1-2*boollist\n",
"\t\tenergy += dE*boollist\n",
"\t\tenergylist[step] = energy\n",
"\tvalidElist = energylist[moves//2:]/(N*N)\n",
"\temc = np.mean(validElist,axis=0)\n",
"\tS=np.std(validElist, ddof=1, axis=0)\n",
"\thalfn = validElist.size\n",
"\terrbar = S*t.isf(0.05,halfn-1)/np.sqrt(halfn)\n",
"\treturn emc,errbar"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
},
"tags": []
},
"source": [
"N = 8"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"ExecuteTime": {
"end_time": "2022-04-19T14:30:32.853919Z",
"start_time": "2022-04-19T14:30:24.259306Z"
}
},
"outputs": [
{
"data": {
"application/vnd.jupyter.widget-view+json": {
"model_id": "632a9a3f02f74660a3b11a4d0e3b33d9",
"version_major": 2,
"version_minor": 0
},
"text/plain": [
"Output()"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/html": [
"\n"
],
"text/plain": []
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/html": [
"\n",
"\n"
],
"text/plain": [
"\n"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"image/svg+xml": [
"\n",
"\n",
"\n"
],
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"T=np.arange(0.5, 5, step=0.1)\n",
"N=8\n",
"elist, errbar = Ising2D_E_vec(T, 200000, N=N)\n",
"if N in [2,4,8]:\n",
"\tthElist = E_theory(T,N=N)\n",
"\tplt.plot(T,thElist)\n",
"plt.errorbar(T, elist, yerr=errbar, fmt=\"None\")\n",
"plt.scatter(T,elist, marker=\"x\", c=\"r\", zorder=2.5)\n",
"plt.title(\"E/N^2 vs T\")\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
},
"tags": []
},
"source": [
"##### (2) Magnetization $M$"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"$$ M = \\left< \\sum_i \\sigma_i \\right> $$"
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {
"ExecuteTime": {
"end_time": "2022-04-19T14:31:11.370171Z",
"start_time": "2022-04-19T14:31:11.363989Z"
},
"slideshow": {
"slide_type": "fragment"
},
"tags": []
},
"outputs": [],
"source": [
"from scipy.stats import chi2,halfnorm,t\n",
"def Ising2D_M_vec(T,moves=1000000, N=16):\n",
"\tJ = 1\n",
"\tB = 0\n",
"\tNT=T.size\n",
"\n",
"\tslist = np.ones((N,N,NT), dtype=int)\n",
"\tMlist = np.empty((moves, NT))\n",
"\tM = N*N\n",
"\n",
"\tfor step in track(range(moves)):\n",
"\t\t[i,j] = rng.integers(N,size=2)\n",
"\t\tdE = 2*J*(slist[(i-1)%N,j] + slist[(i+1)%N,j] + slist[i,(j-1)%N] + slist[i,(j+1)%N])*slist[i,j]\n",
"\t\tboollist = rng.random() < np.exp(-dE/T)\n",
"\t\tslist[i,j] *= 1-2*boollist\n",
"\t\tM += 2*slist[i,j]*boollist\n",
"\t\tMlist[step] = M\n",
"\t# eth = -J*(1+2*(2*(np.tanh(2*J/T)**2)-1)*ellipk(2*np.tanh(2*J/T)/np.cosh(2*J/T)))/np.tanh(2*J/T)\n",
"\tvalidMlist = Mlist[moves//2:]/(N*N)\n",
"\tMmc = np.mean(validMlist,axis=0)\n",
"\tS=np.std(validMlist, ddof=1, axis=0)\n",
"\thalfn = validMlist.size\n",
"\terrbar = S*t.isf(0.00135,halfn-1)/np.sqrt(halfn)\n",
"\treturn Mmc,errbar"
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {
"ExecuteTime": {
"end_time": "2022-04-19T14:31:44.065707Z",
"start_time": "2022-04-19T14:31:14.334542Z"
},
"slideshow": {
"slide_type": "fragment"
},
"tags": []
},
"outputs": [
{
"data": {
"application/vnd.jupyter.widget-view+json": {
"model_id": "65d805042537458db00fc80e0d7ad4eb",
"version_major": 2,
"version_minor": 0
},
"text/plain": [
"Output()"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/html": [
"\n"
],
"text/plain": []
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/html": [
"\n",
"\n"
],
"text/plain": [
"\n"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"image/svg+xml": [
"\n",
"\n",
"\n"
],
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"T=np.arange(0.5, 5, step=0.1)\n",
"Tt= np.arange(0.5,5,step = 0.02)\n",
"N=16\n",
"Mlist, errbar = Ising2D_M_vec(T, 1000000, N=N)\n",
"a = 1-np.power(np.sinh(2/Tt),-4)\n",
"thMlist = np.power(a*(a>0),1/8)\n",
"plt.plot(Tt,thMlist)\n",
"plt.errorbar(T, Mlist, yerr=errbar, marker=\"x\")\n",
"plt.title(\"M/N^2 vs T\")\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Metropolis MC method works not very well around the critical temp!"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
},
"tags": []
},
"source": [
"##### (3) heat capacity $C$"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"$$ C = \\frac{\\partial \\left< E \\right>}{\\partial T} = \\frac{(\\Delta E)^2}{T^2} $$"
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {
"ExecuteTime": {
"end_time": "2022-04-19T14:31:44.075715Z",
"start_time": "2022-04-19T14:31:44.070245Z"
},
"slideshow": {
"slide_type": "fragment"
},
"tags": []
},
"outputs": [],
"source": [
"from scipy.stats import chi2,halfnorm,t\n",
"def Ising2D_C_vec(T,moves=1000000,N=16):\n",
"\tJ = 1\n",
"\tB = 0\n",
"\tNT=T.size\n",
"\n",
"\tslist = np.ones((N,N,NT), dtype=int)\n",
"\tenergylist = np.empty((moves,NT))\n",
"\tenergy = - 2*J * N * N\n",
"\n",
"\tfor step in track(range(moves)):\n",
"\t\t[i,j] = rng.integers(N,size=2)\n",
"\t\tdE = 2*J*(slist[(i-1)%N,j] + slist[(i+1)%N,j] + slist[i,(j-1)%N] + slist[i,(j+1)%N])*slist[i,j]\n",
"\t\tboollist = rng.random() < np.exp(-dE/T)\n",
"\t\tslist[i,j] *= 1-2*boollist\n",
"\t\tenergy += dE*boollist\n",
"\t\tenergylist[step] = energy\n",
"\tvalidElist = energylist[moves//2:]/(N*N)\n",
"\thalfn = validElist.size\n",
"\tS=np.std(validElist, ddof=1, axis=0)\n",
"\tcmc = S*S/(T*T)\n",
"\talpha = 0.01\n",
"\tc1 =chi2.isf(alpha/2, halfn - 1)\n",
"\tc2 = chi2.isf(1-alpha/2, halfn - 1)\n",
"\terrbar = np.array([(1-(halfn - 1)/c1)*cmc,((halfn-1)/c2 - 1)*cmc])\n",
"\treturn cmc,errbar"
]
},
{
"cell_type": "code",
"execution_count": 19,
"metadata": {
"ExecuteTime": {
"end_time": "2022-04-19T14:32:12.700093Z",
"start_time": "2022-04-19T14:31:44.076945Z"
},
"slideshow": {
"slide_type": "fragment"
},
"tags": []
},
"outputs": [
{
"data": {
"application/vnd.jupyter.widget-view+json": {
"model_id": "d3a8af477b4f4da2b3ce86b171558aa1",
"version_major": 2,
"version_minor": 0
},
"text/plain": [
"Output()"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/html": [
"\n"
],
"text/plain": []
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/html": [
"\n",
"\n"
],
"text/plain": [
"\n"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"image/svg+xml": [
"\n",
"\n",
"\n"
],
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"T = np.arange(0.5, 10,step=0.2)\n",
"C,errbar = Ising2D_C_vec(T)\n",
"plt.errorbar(T, C, yerr=errbar, marker=\"x\")\n",
"plt.title(\"C0 vs T\")\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
},
"tags": []
},
"source": [
"##### (4) susceptibility $\\chi$"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"$$ \\chi=\\frac{\\partial M}{\\partial T}=\\frac{(\\Delta M)^{2}}{T}=\\frac{\\langle M^{2}\\rangle-\\langle M\\rangle^{2}}{T} $$"
]
},
{
"cell_type": "code",
"execution_count": 65,
"metadata": {
"slideshow": {
"slide_type": "fragment"
},
"tags": []
},
"outputs": [],
"source": [
"from scipy.stats import chi2\n",
"def Ising2D_chi_vec(T,moves=1000000,N=16):\n",
"\tJ = 1\n",
"\tB = 0\n",
"\tNT=T.size\n",
"\n",
"\tslist = np.ones((N,N,NT), dtype=int)\n",
"\tMlist = np.empty((moves,NT))\n",
"\tM = J * N * N\n",
"\n",
"\tfor step in track(range(moves)):\n",
"\t\t[i,j] = rng.integers(N,size=2)\n",
"\t\tdE = 2*J*(slist[(i-1)%N,j] + slist[(i+1)%N,j] + slist[i,(j-1)%N] + slist[i,(j+1)%N])*slist[i,j]\n",
"\t\tboollist = rng.random() < np.exp(-dE/T)\n",
"\t\tslist[i,j] *= 1-2*boollist\n",
"\t\tM += 2*slist[i,j]*boollist\n",
"\t\tMlist[step] = M\n",
"\tvalidMlist = Mlist[moves//2:]/(N*N)\n",
"\thalfn = validMlist.size\n",
"\tS=np.std(validMlist, ddof=1, axis=0)\n",
"\tchimc = S*S/t\n",
"\talpha = 0.01\n",
"\tc1 =chi2.isf(alpha/2, halfn - 1)\n",
"\tc2 = chi2.isf(1-alpha/2, halfn - 1)\n",
"\terrbar = np.array([(1-(halfn - 1)/c1)*chimc,((halfn-1)/c2 - 1)*chimc])\n",
"\treturn chimc,errbar"
]
},
{
"cell_type": "code",
"execution_count": 67,
"metadata": {
"slideshow": {
"slide_type": "fragment"
},
"tags": []
},
"outputs": [
{
"data": {
"text/html": [
"Working... ━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 0% -:--:--\n",
"\n"
],
"text/plain": [
"Working... \u001b[38;5;237m━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━\u001b[0m \u001b[35m 0%\u001b[0m \u001b[36m-:--:--\u001b[0m\n"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/html": [
"\n"
],
"text/plain": []
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/html": [
"\n",
"\n"
],
"text/plain": [
"\n"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"image/svg+xml": [
"\n",
"\n",
"\n"
],
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"T = np.arange(0.5, 6,step=0.2)\n",
"chi,errbar = Ising2D_chi_vec(T)\n",
"plt.errorbar(T, chi, yerr=errbar, marker=\"x\")\n",
"plt.title(\"chi vs T\")\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
},
"tags": []
},
"source": [
"#### Run over T"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
},
"tags": []
},
"source": [
"Let $T$ vary slowly from high to low."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"# Ising2D_runover_T.py\n",
"# too long to show..."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
},
"tags": []
},
"source": [
"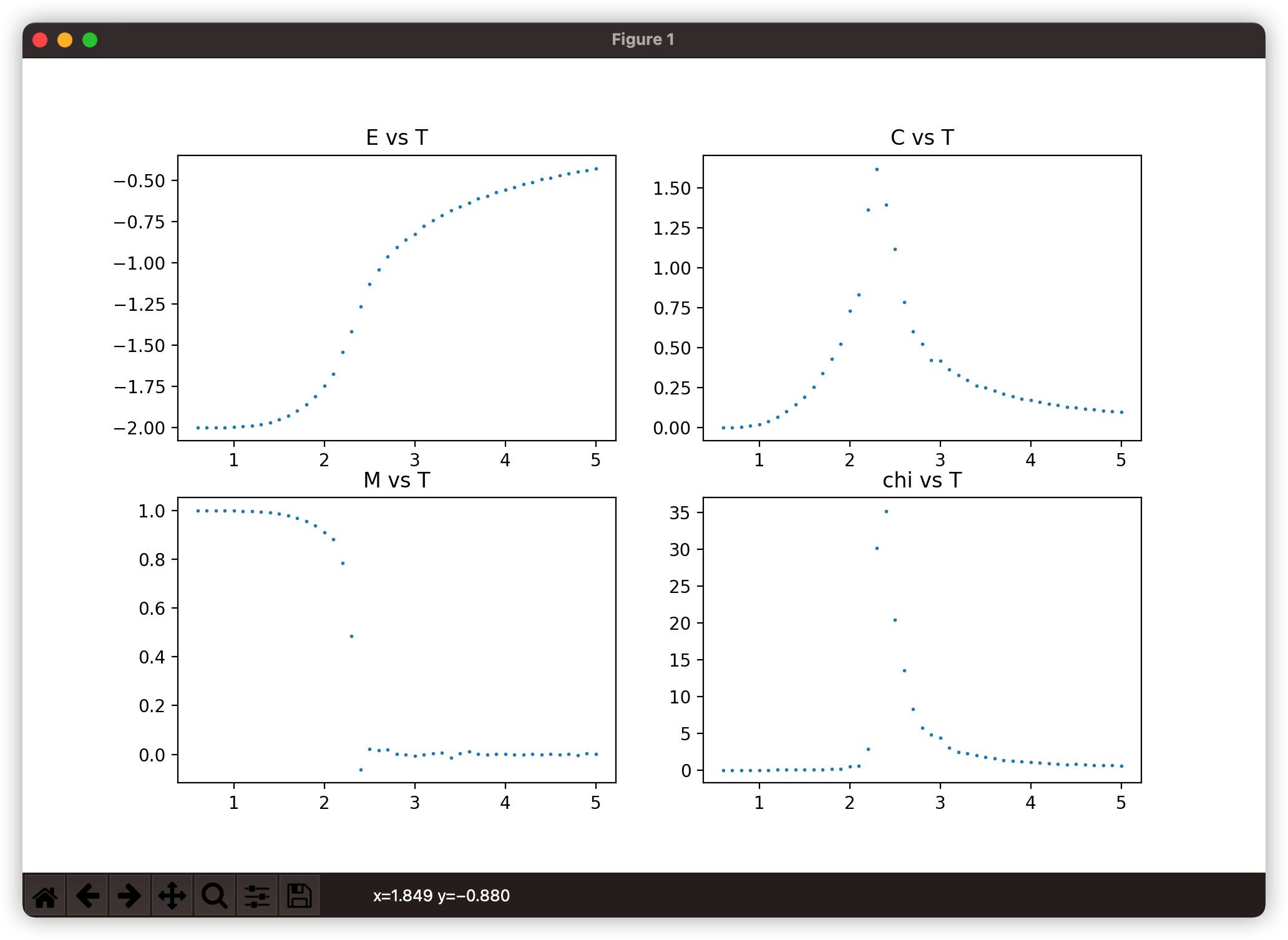"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
},
"tags": []
},
"source": [
"#### Run over $B$"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We relax the $B=0$ condition, and fix $T=1$ (low temperature) --- Just like magnetize an iron block!"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"ExecuteTime": {
"end_time": "2022-04-19T15:09:04.866346Z",
"start_time": "2022-04-19T15:08:58.734467Z"
},
"tags": []
},
"outputs": [
{
"data": {
"application/vnd.jupyter.widget-view+json": {
"model_id": "39ca76c530f64040974f36f52d529afe",
"version_major": 2,
"version_minor": 0
},
"text/plain": [
"Output()"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/html": [
"\n"
],
"text/plain": []
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"image/svg+xml": [
"\n",
"\n",
"\n"
],
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# run external Ising2D_runover_B.py\n",
"%config InlineBackend.figure_format='svg'\n",
"import Ising2D_runover_B"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We can see the path dependence!"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
},
"tags": []
},
"source": [
"## Conclusion"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
},
"tags": []
},
"source": [
"- The Metropolis MC is very fast"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
},
"tags": []
},
"source": [
"- It's also accuracy, except $T \\sim T_c$"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
},
"tags": []
},
"source": [
"- The code can be easily reuse for another quantity"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
},
"tags": []
},
"source": [
"- Depends on:\n",
" - `rng`, random number generator\n",
" - a good step $\\Delta x$"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
},
"tags": []
},
"source": [
"## Thanks!"
]
}
],
"metadata": {
"celltoolbar": "无",
"kernelspec": {
"display_name": "Python 3 (ipykernel)",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.10.11"
},
"latex_envs": {
"LaTeX_envs_menu_present": true,
"autoclose": true,
"autocomplete": true,
"bibliofile": "biblio.bib",
"cite_by": "apalike",
"current_citInitial": 1,
"eqLabelWithNumbers": true,
"eqNumInitial": 1,
"hotkeys": {
"equation": "Ctrl-E",
"itemize": "Ctrl-I"
},
"labels_anchors": false,
"latex_user_defs": true,
"report_style_numbering": false,
"user_envs_cfg": false
}
},
"nbformat": 4,
"nbformat_minor": 4
}